What is Monte Carlo Simulation?

Monte Carlo Simulation is a process of using probability curves to determine the likelihood of an outcome.  You may scratch your head here and say…  “Hey Rick, a distribution curve has an array of values.  So how exactly do I determine the likelihood of an outcome?”  And better yet, how do I do that in Microsoft Excel without any special add-ins

Thought you would never ask.

This is done by running the simulation thousands of times and analyzing the distribution of the output.  This is particularly important when you are analyzing the output of several distribution curves that feed into one another.

Example:

• # of Units Sold may have a distribution curve
• multiplied by Market price, which may have another distribution curve
• minus variable wages which have another curve
• etc., etc.

Once all these distributions are intermingled, the output can be quite complex.  Running thousands of iterations (or simulations) of these curve may give you some insights.  This is particularly useful in analyzing potential risk to a decision.

Describe Monte Carlo

When describing Monte Carlo Simulation, I often refer to the 1980’s movie War Games, where a young Mathew Broderick (before Ferris Bueller) is a hacker that uses his dial up modem to hack into the Pentagon computers and start World War 3.  Kind of.  He then had the Pentagon computers do many simulations of the games Tic Tac Toe to teach the computer that no one will will a nuclear war – and save the world in the process.

Thanks Ferris. You’re a hero.

Here’s a glimpse of the movie to show you big time Monte Carlo in action.  I am assuming that you will overlook the politics, the awkward man hugging and of course, Dabney Coleman.

The Monte Carlo Simulation Formula

Distribution Curves

There are various distribution curves you can use to set up your Monte Carlo simulation.  And these curves may be interchanged based on the variable.  Microsoft doesn’t have a formula called “Do Monte Carlo Simulation” in the menu bar 🙂

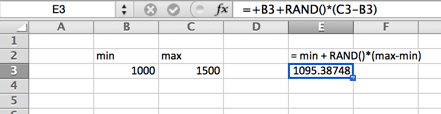
Uniform Distribution

In a uniform distribution, there is equal likelihood anywhere between the minimum and a maximum.  A uniform distribution looks like a rectangle.

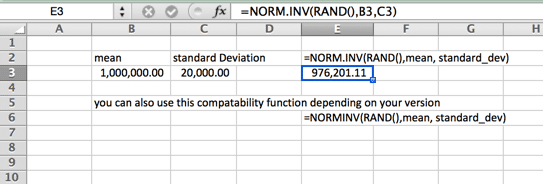
Normal (Gaussian) Distribution

This is also your standard bell shaped curve.  This Monte Carlo Simulation Formula is characterized by being evenly distributed on each side (median and mean is the same – and no skewness).  The tails of the curve go on to infinity.  So this may not be the ideal curve for house prices, where a few top end houses increase the average (mean) well above the median, or in instances where there is a hard minimum or maximum.  An example of this may be the minimum wage in your locale. Please note that the name of the function varies depending on your version.

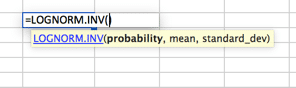
Lognormal Distribution

A distribution where the logarithm is normally distributed with the mean and standard deviation.  So the setup is similar to the normal distribution, but please note that the mean and standard_dev variables are meant to represent the logarithm.

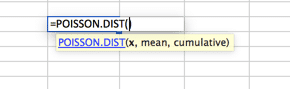
Poisson Distribution

This is likely the most underutilized distribution.  By default, many people use a normal distribution curve when Poisson is a better fit for their models.  Poisson is best described when there is a large distribution near the very beginning that quickly dissipates to a long tail on one side.  An example of this would be a call center, where no calls are answered before second ZERO.  Followed by the majority of calls answered in the first 2 intervals (say 30 and 60 seconds) with a quick drop off in volume and a long tail, with very few calls answered in 20 minutes (allegedly).

The purpose here is not to show you every distribution possible in Excel, as that is outside the scope of this article.  Rather to ensure that you know that there are many options available for your Monte Carlo Simulation.  Do not fall into the trap of assuming that a normal distribution curve is the right fit for all your data modeling.  To find more curves, to go the Statistical Functions within your Excel workbook and investigate.  If you have questions, pose them in the comments section below.

Building The Model

For this set up we will assume a normal distribution and 1,000 iterations.

Input Variables

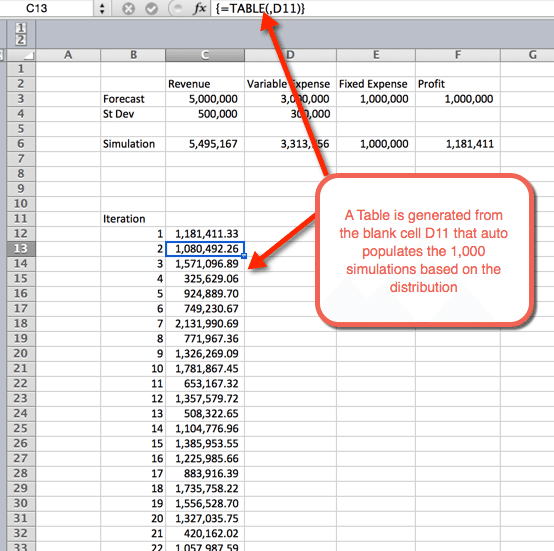
The setup assumes a normal distribution. A normal distribution requires three variables; probability, mean and standard deviation.  We will tackle the mean and standard deviation in our first step.  I assume a finance forecasting problem that consists of Revenue, Variable and Fixed Expenses.  Where Revenue minus Variable Expenses minus Fixed Expenses equals Profit.  The Fixed expenses are sunk cost in plant and equipment, so no distribution curve is assumed.  Distribution curves are assumed for Revenue and Variable Expenses.

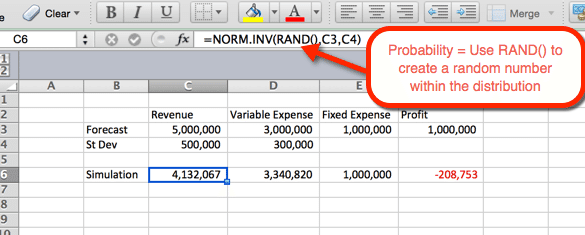
First Simulation

The example below indicates the settings for Revenue.  The formula can be copy and pasted to cell D6 for variable expenses.  For Revenue and expenses we you the function NORM.INV() where the parameters are:

• Probability = the function RAND() to elicit a random number based on the other criteria within the distribution.
• Mean = The mean used in the Step 1.  For Revenue it is C3.
• Standard Deviation = The Standard Deviation used in Step 1.  For Revenue it is C4

Since RAND() is used as the probability, a random probability is generated at refresh.  We will use this to our advantage in the next step.

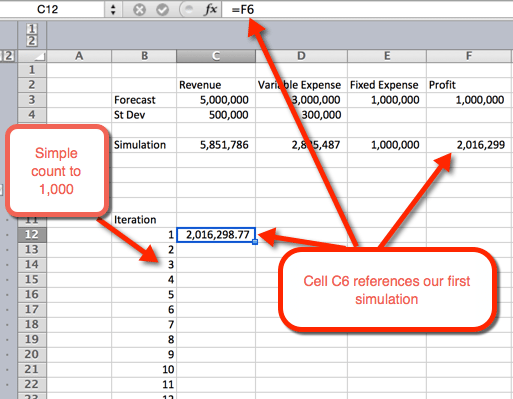
1,000 Simulations

There are several ways to do 1,000 or more variations.  The simplest option is to take the formula from step #2 and make it absolute.  Then copy and paste 1,000 times.  That’s simple, but not very fancy.  And if Ferris Bueller can save the world by showing a new Tic Tac Toe game to a computer, then we can spice up this analysis as well. Let’s venture into the world of tables.

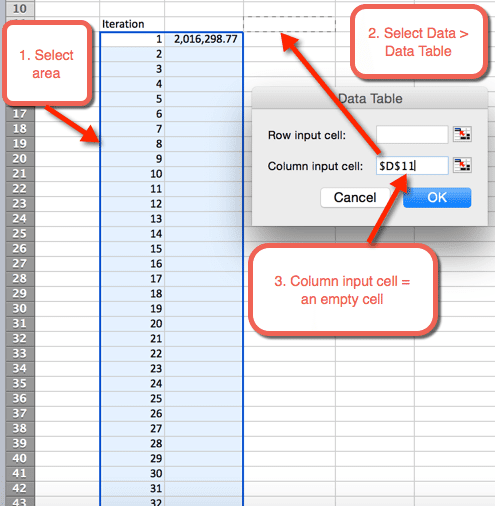
• First we want to create an outline for a table.  We do this by listing the numbers 1 to 1,000 in rows.  In the example image below, the number list starts in B12.
• in the next column, in cell C12, we will reference the first iteration.

• Next highlight the area where we want to house the 1,000 iterations
• Select Data > Data Tables
• For Column input cell: Select a blank cell.  In the download file, cell D11 is selected
• Select OK

• Once OK is selected from the previous step, a table is inserted that autopopulates the 1,000 simulations

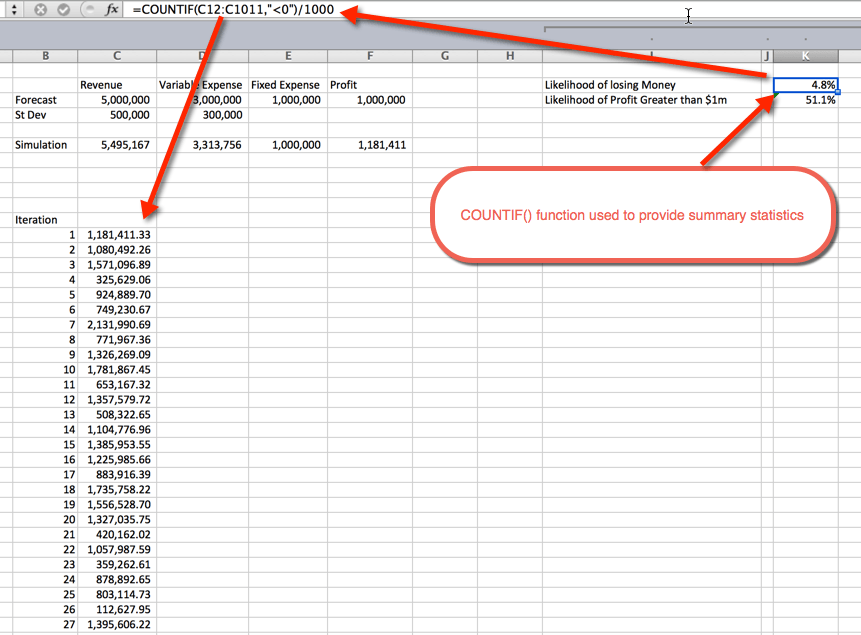
Summary Statistics

Once the simulations are run, it is time to gather summary statistics.  This can be done a number of ways.  In this example I used the COUNTIF() function to determine the percentage of simulations that are unprofitable, and the likelihood of a profit greater than $1 Million.  As expected, the likelihood of greater than $1M hovers around 50%.  This is because we used normal distribution curves that are evenly distributed around the mean, which was $1M.  The likelihood of losing money is 4.8%.  This was gathered by using the COUNTIF() function to count the simulations that were less than zero, and dividing by the 1,000 total iterations.

Download

[thrive_link color=’teal’ link=’https://excel.tv/wp-content/uploads/monte-carlo-simulation.xlsx’ target=’_blank’ size=’small’ align=’aligncenter’]Download The Monte Carlo Simulation FIle[/thrive_link]

Now What?

In the video above, Oz asks about the various uses for Monte Carlo Simulation.  What have you used it for?  Are there any specific examples that you can share with the group?  If so, leave a note below in the comments section.  Also, feel free to sign up for our newsletter, so that you can stay up to date as new Excel.TV shows are announced.  Leave me a message below to stay in contact.

Bloggers Love Comments

[thrive_link color=’teal’ link=’https://excel.tv/monte-carlo-simulation-excel-tutorial-download/#comments’ target=’_self’ size=’small’ align=’aligncenter’]Leave A Comment[/thrive_link]